The circle of fifths explained: how to use it in your guitar playing

You may or may not have heard the term 'circle of fifths' before. Either way, it’s something you’re going to need to know about at some point. It’s an essential concept in music theory, songwriting and composition for both electric and acoustic guitar players.

What Is the circle of fifths?

The circle of fifths is a principle in music theory that begins from the note of C and the key of C major (because it has no sharps or flats) and repeatedly moves up in steps of a perfect fifth, through every key, until it returns to C major again.

Because the above sounds like a bit of a mouthful, here’s a handy table showing how this works and some other useful information:

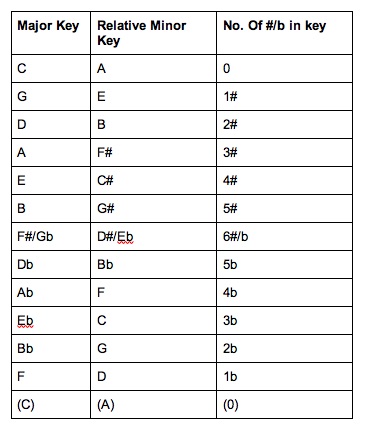
Notice that going down the major keys means moving up a perfect fifth each time (i.e. C to G is a perfect fifth, then G to D is another, D to A is another and so on). Notice also that going down these major keys’ relative minor keys (found three semitones down from the relative major) also means moving up in perfect fifths (A > E > B etc)

Doing this naturally arranges the keys in a sequence, as you’ll see, of moving up through ‘the sharp keys.’ For example, C major has no sharps, G major has "one sharp" (F#) and so on. It then works down the flat keys—from Gb major (six flats) down through F major (one flat) to C major again.

You’ll also notice that if you work upwards through the table instead of down, everything jumps in perfect fourths rather than perfect fifths. Besides being aware that occasionally people look at it this way around and call it “the circle of fourths," this is just an incidental fact of the symmetry of music theory that you should note and remember.

What can I learn from the circle of fifths?

Note that a perfect fifth is a perfect fourth when flipped on its head, and use this to learn (if you don’t know already) how many sharps or flats are in each key, and their sequences (i.e. ‘one sharp is G major, two is D, three is A and so on).

It’s also good for visualizing and remembering the pairings of relative major/minor keys, and to learn why you might choose one enharmonic equivalent over another. Remember, enharmonics are different names for the same note. For example, F# and Gb are enharmonic equivalents - the same note, but two different names. The reason why - if given the choice - we would generally choose to call it F# is that, as you’ll see on the table above, F# has three sharps, whereas Gb has six flats. When reading or writing standard sheet music style notation, treating it as F# makes it a lot easier!

Following on from this, you’ll notice that most of the time, if you pick any sharp or flat given in the table above and look at its number of sharps or flats, when you convert that note to its enharmonic equivalent, the number of sharps or flats will be higher. This is the reason that the particular version of the enharmonic given has been chosen in the first place.

How can I use the circle of fifths?

Probably the single biggest way to use the circle of fifths is in modulation (or changing key) in your songwriting and composition.

The perfect cadence

A perfect cadence, also called a 5-1 ("Five One") is the name for a two chord sequence of chord 5 in a key, followed by chord 1 in that —e.g. a G major chord (chord 5) to a C major chord (chord 1) in C major.

The perfect cadence is known for creating a strong, natural resolution, and being a very effective way to finish a section or piece.

Changing key using the perfect cadence

One of the most straightforward ways of changing key involves the perfect cadence.

Take this example, for instance: You’re playing in the key of C major, and you want to change to the key of Bb major. So, you take your chord progression in your current key of C major to an F major chord (chord 4 in C major). This F major chord is chord 5 in Bb major.

From this F chord, you don’t continue by reverting back to the chords in the key of C, you instead land on Bb major, and have therefore played a perfect cadence (i.e. F to Bb major is a 5-to-1 progression in Bb major). Thus, you are now smoothly in the key of Bb major and can continue from there using its inherent chords.

There are many links and connections to make with the circle of fifths, and many ways in which it can help you to re-frame and understand music theory, songwriting and composition. So I encourage you to keep learning and exploring. But hopefully this has given you a good basic overview of what the circle of fifths is and some of the main ways it can be useful. Good luck, and enjoy!

Alex Bruce is a writer for Guitartricks.com. GuitarTricks.com has over 11,000 lessons covering everything a beginner guitar needs to know to get started, as well as more complicated techniques like tapping, sweeping, scales, and more.